数学教师专业发展研究：三棱锥模型与策略

1. 背景与问题

数学教师的专业发展（Professional Development, PD）是提高教学质量和学生学习效果的关键。然而，随着PD规模的扩大，促进者（facilitators）的作用变得尤为重要。目前，关于促进者的研究相对较少，本文旨在通过“三棱锥模型”（Three-Tetrahedron Model, 3T-Model）系统化现有研究，并提出支持促进者的研究策略。

2. 理论框架：三棱锥模型（3T-Model）

三棱锥模型是一个多层次、多维度的框架，用于分析和设计数学教师的专业发展。它包括三个层次：

课堂层次：关注学生的学习和教师的教学。
教师PD层次：关注教师的学习和促进者的作用。
促进者PD层次：关注促进者的学习和发展。

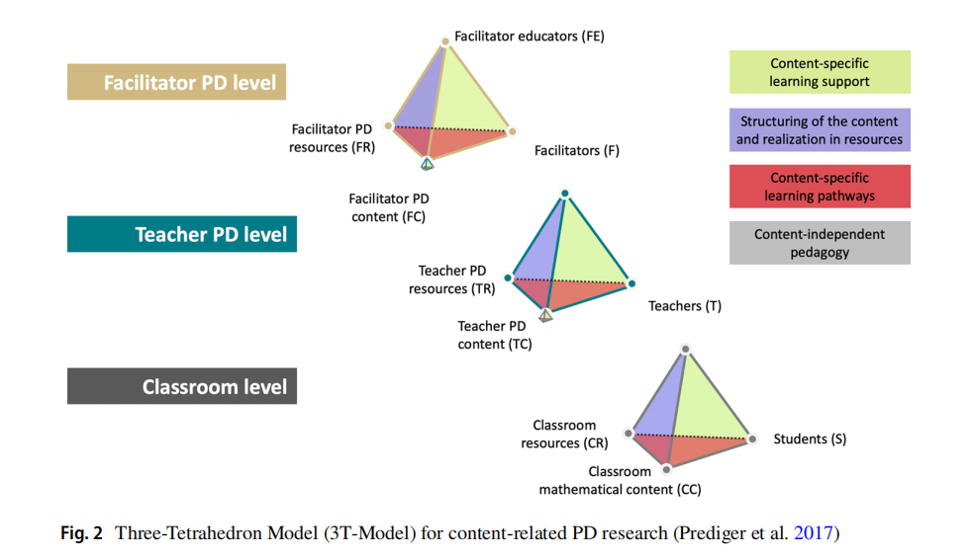
图1：三棱锥模型（3T-Model）

三棱锥模型的核心是“教学四面体”（didactical tetrahedron），它包括四个要素：教师、学生、内容和资源。这些要素之间的关系构成了教学和学习的复杂性。

3. 三种研究策略

文章提出了三种研究策略，用于支持数学教师专业发展的设计和研究：

3.1 提升策略（Lifting Strategy）

提升策略是将课堂层面的设计和研究方法“提升”到教师PD或促进者PD层面，利用结构上的类比性。

例如，课堂中使用视频支持教师观察学生行为的方法，可以提升到促进者PD中，帮助促进者观察教师的学习行为。

3.2 嵌套策略（Nesting Strategy）

嵌套策略是在设计PD时，将课堂四面体的复杂性嵌套到教师PD内容中，再将教师PD的复杂性嵌套到促进者PD内容中。

例如，设计一个关于代数工具使用的教师PD时，需要考虑学生在课堂中的学习路径和常见误解。

3.3 拆解策略（Unpacking Strategy）

拆解策略是在研究PD时，将PD内容拆解为四面体的各个要素，深入分析其内容特定性。

例如，研究促进者在PD中的表现时，可以拆解为他们对数学内容的理解、对教学资源的使用以及对教师学习路径的支持。

4. 案例分析

案例1：Swan的任务型PD研究

Swan的研究关注任务型PD的设计和效果。研究的核心是通过设计丰富的代数任务，帮助教师改进教学实践。

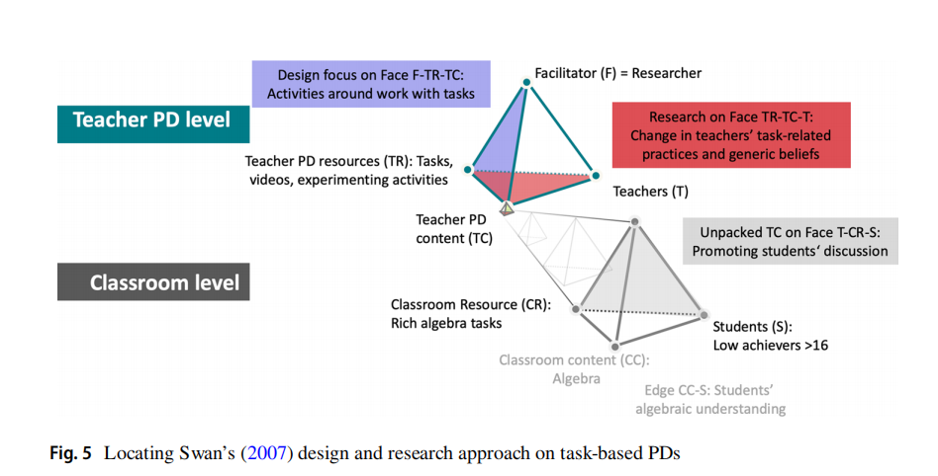
图2：Swan的任务型PD研究

Swan的研究展示了如何通过任务设计提升教师的教学实践。研究的重点是：

设计丰富的代数任务，激发学生的认知活动。
通过视频案例展示任务在课堂中的实际应用。
促进教师反思和改进教学实践。

研究的局限性在于对教师信念的变化分析较为通用，未深入探讨数学学习内容的具体影响。

案例2：Borko的问题解决循环PD研究

Borko的研究关注促进者如何通过问题解决循环模型支持教师的专业发展。

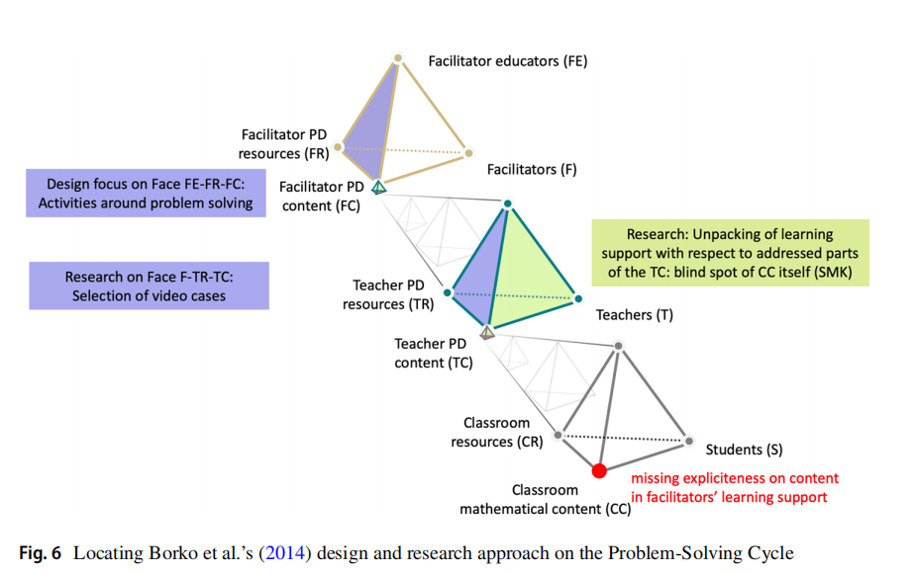
图3：Borko的问题解决循环PD研究

Borko的研究展示了如何通过问题解决循环模型支持教师的专业发展。研究的重点是：

设计包含数学丰富任务的PD工作坊，帮助教师解决实际教学问题。
通过视频案例分析教师的教学实践和学生思维。
促进教师反思和改进教学策略。

研究的局限性在于促进者在支持教师深入分析数学内容和教学实践方面存在困难。

5. 总结与展望

三棱锥模型为数学教师专业发展提供了一个系统化的框架，帮助研究者和设计者明确研究重点、识别研究空白，并为促进者提供支持。通过提升、嵌套和拆解三种策略，可以更好地理解和设计数学教师的专业发展项目。

未来的研究可以进一步探索三棱锥模型在不同教育背景下的应用，并结合社会文化因素，完善模型的理论框架。